knn 알고리즘을 이해하는 데에 유용한 사이트와 그 사용법을 소개합니다.
vision.stanford.edu/teaching/cs231n-demos/knn/
접속하면, 아래와 같은 페이지가 나타납니다.
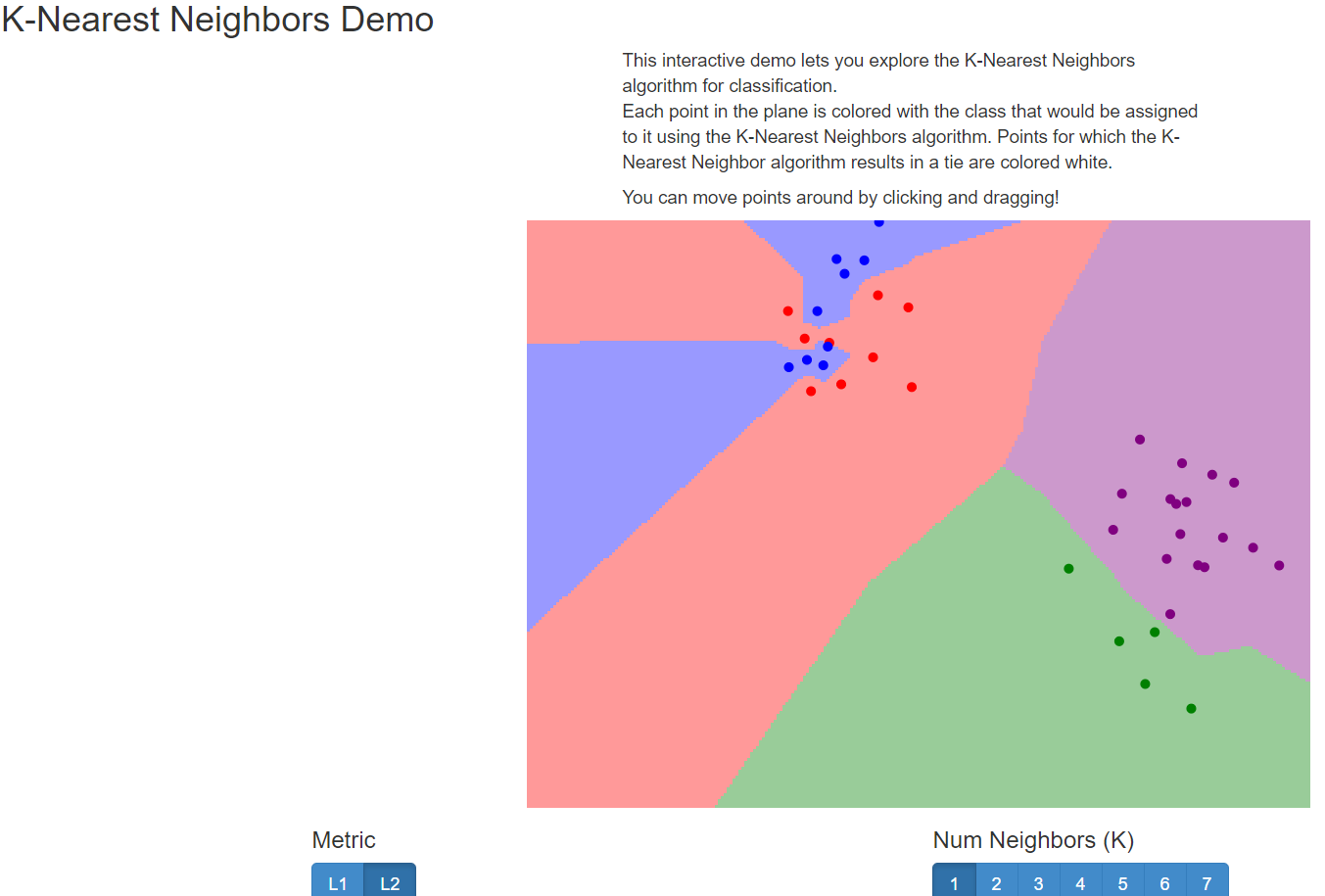
페이지 하단의 메뉴의 버튼들을 클릭하는 것으로 간단하게 조건을 바꿀 수 있습니다.
우선, 1. 첫번째 Metric 에서는 거리를 구하는 방법을 정할 수 있습니다.

L1: 맨해튼 거리 공식
L2: 유클리드 거리 공식
이 두가지를 의미합니다. (보통 L2 설정)
2. Num classes 는 그룹, 분류의 갯수를 정합니다.

3. Num Neighbors (K) 는 바로 최근접 이웃의 갯수를 정합니다.
보통 홀수로 정하며, 주변 K개의 데이터의 결과에서 다수결의 원칙에 따라 결정됩니다.
4. Num Points (K) 는 데이터의 수를 정합니다.

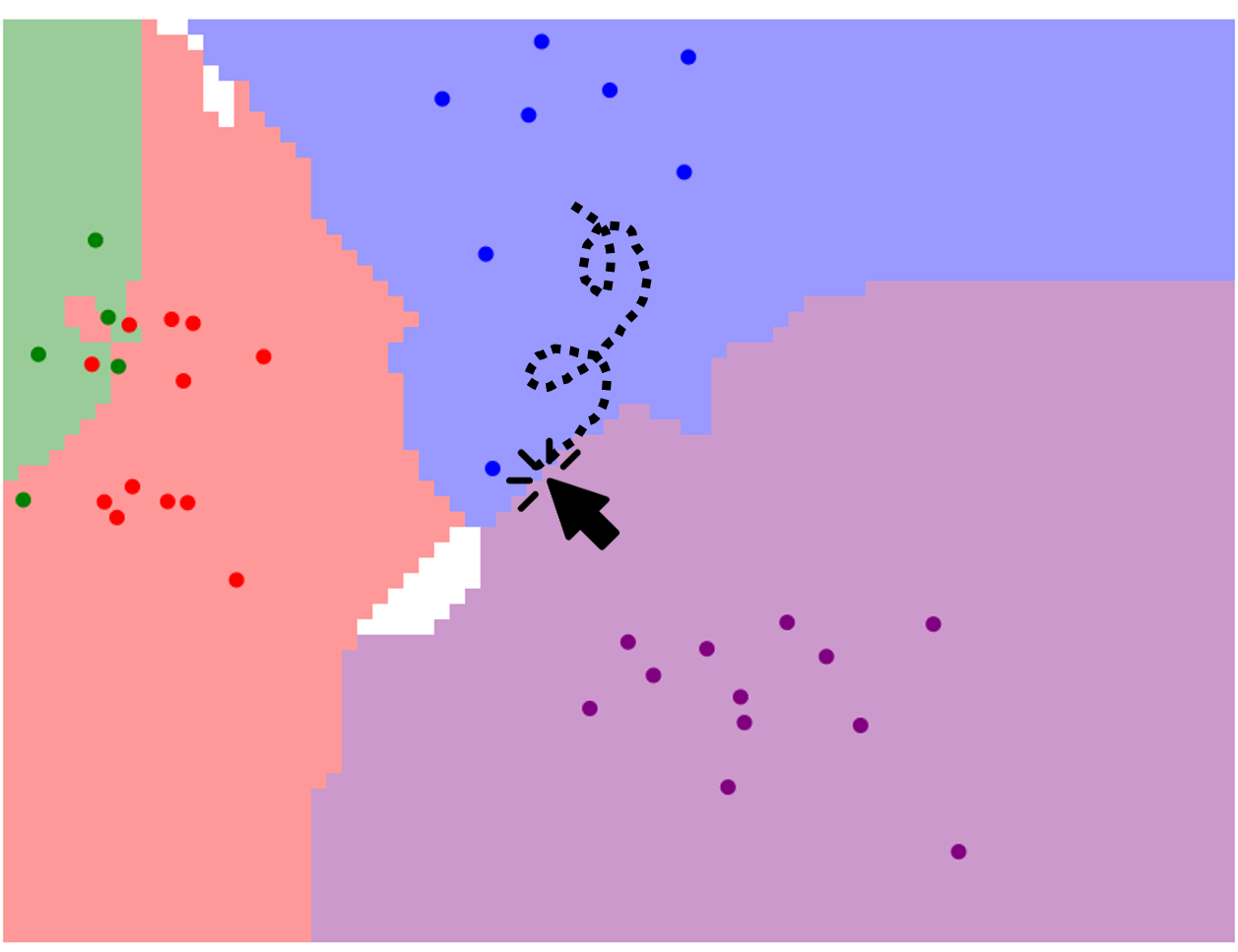
각 데이터의 값은 마우스로 점을 드래그 하여 옮길 수 있습니다.
어렵지 않게 k-nn 알고리즘의 작동 원리를 시각화하여 살펴볼 수 있어 학생들 학습에도 유용해보입니다!
k-nearest neighbors algorithm

From Wikipedia, the free encyclopedia
Jump to navigationJump to search
Not to be confused with k-means clustering.
In statistics, the k-nearest neighbors algorithm (k-NN) is a non-parametric classification method first developed by Evelyn Fix and Joseph Hodges in 1951,[1] and later expanded by Thomas Cover.[2] It is used for classification and regression. In both cases, the input consists of the k closest training examples in data set. The output depends on whether k-NN is used for classification or regression:
- In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of that single nearest neighbor.
- In k-NN regression, the output is the property value for the object. This value is the average of the values of k nearest neighbors.
k-NN is a type of classification where the function is only approximated locally and all computation is deferred until function evaluation. Since this algorithm relies on distance for classification, if the features represent different physical units or come in vastly different scales then normalizing the training data can improve its accuracy dramatically.[3][4]
Both for classification and regression, a useful technique can be to assign weights to the contributions of the neighbors, so that the nearer neighbors contribute more to the average than the more distant ones. For example, a common weighting scheme consists in giving each neighbor a weight of 1/d, where d is the distance to the neighbor.[5]
The neighbors are taken from a set of objects for which the class (for k-NN classification) or the object property value (for k-NN regression) is known. This can be thought of as the training set for the algorithm, though no explicit training step is required.
A peculiarity of the k-NN algorithm is that it is sensitive to the local structure of the data.
출처 : en.wikipedia.org/wiki/K-nearest_neighbors_algorithm
<i>k</i>-nearest neighbors algorithm
In statistics, the k-nearest neighbors algorithm (k-NN) is a non-parametric classification method first developed by Evelyn Fix and Joseph Hodges in 1951,[1] and later expanded by Thomas Cover.[2] It is used for classification and regression. In both cases
en.wikipedia.org
'AI , 컴퓨터 , 대학원 > 딥러닝 공부' 카테고리의 다른 글
| [용어] 초보자를 위한 머신러닝 용어 _ 특성, 인스턴스(instance) 등 (0) | 2023.02.19 |
|---|---|
| 14주차 EOS 란? (자연어처리) / np.zeros() / iterrows (0) | 2021.05.29 |
| 파이썬으로 배우는 알고리즘 트레이딩 (0) | 2021.02.15 |

